Have you ever looked at a giant ship and wondered how such a heavy object made of steel floats in water? I know I have. As a matter of fact, I still marvel at the science behind giant cruise ships, with thousands of passengers, tons of supplies, and entire theme parks on board, not sinking to the bottom of the ocean! And how about those staggering 20,000 TEU container ships, carrying all the world’s TVs, smart phones, and t-shirts through wind and stormy weather? Well, let’s have a look.

So, how does it float?

For a ship to float, it must have lower density than water. At first sight, this might not make sense, as the steel that ships are made of is not exactly known for its low density. The thing is, the density of an object results from the relationship between its total volume and weight. If the total volume of a ship is large enough in relation to its weight, it has a low density. Simply put, because of all the air spaces inside, a ship has a lower average density than water, despite the heavy materials it is made of.

The weight of water a ship displaces gives it buoyancy – a force acting against gravity on a body immersed in liquids or gases. This force is caused by the displacement, or pushing aside, of the surrounding medium (water) and corresponds to the weight of the deformed fluid. This relation between an object and the fluid it is immersed in is known as the Archimedes’ Principle. It applies in the same way, whether we are dealing with a DIY wooden canoe or a giant container ship. A ship floats because the submersed part of it is lighter than the displaced water, and the total weight of the ship equals the total weight of the water it displaces.

However, it is not enough for a ship to simply float in a static state. It also needs to stay upright while sailing through the water in various conditions, and this is where it gets a lot more interesting.

How does it stay upright?

In shipbuilding and design, the term stability refers to the property of a floating body, such as a vessel, to maintain an upright floating position in still waters, or to right itself up again in rough waters. Several key factors determine the individual stability of a ship – the hull’s shape and size, as well as its mass and mass distribution, load weight and distribution, cargo behavior (ex. movement of bulk cargo in the holds), the dynamic behavior of the ship (ex. when changing course at high speed), and the free surface on board when cargo holds are only partially filled. External operating conditions that affect stability are wind, swell, drift, water density (saltwater/freshwater), and the risk of an additional load on the ship due to icing of the deck surfaces in cold weather.

The fundamental parameters of a ship’s stability are its center of gravity, center of buoyancy, metacenter, and metacentric height.

To picture the center of gravity, imagine the entire down-acting weight of the ship, concentrated in one point. When the ship is loaded, the center of gravity retains its position within the ship, as long as all the masses in the ship remain in the same place. But if some cargo on board shifts, due to rough seas for example, its motion and new location may change the ship’s center of gravity.

To understand the center of buoyancy, first think of the total upward force, caused by the hydrostatic pressure from the displaced water. Imagine this water trying to get back to its original location before it was displaced. The more water a ship pushes aside, the greater the buoyant force that the water exerts back upon the ship. The buoyant force may act on all parts of the immersed hull, but the side forces act in opposite directions and are of equal magnitude, therefore cancelling each other out and leaving only those forces acting upward on the hull. As there are too many points along the hull on which the upward forces act, mathematically we treat all of them as one single force acting at one single point. It is this point that we call the center of buoyancy. Technically speaking, this is the centroid of the displaced volume of water, i.e. the arithmetic mean position of all the points where buoyant forces act. Consider it as the one point, where the entire displaced water would remain in equilibrium. It is somewhat difficult to visualize this point in the case of water, as water does not stay in one place. So for simplicity, imagine instead trying to balance a piece of cutout cardboard on the tip of a pin. The point where the piece of cardboard would sit in perfect balance on the tip of the pin, is its centroid.

The metacenter is where the two lines of the original center of buoyancy and the newly shifted center of buoyancy intersect, as pictured in the image below. As the center of buoyancy moves laterally when the ship heels, the metacenter typically stays directly above it. The distance between the center of gravity and the metacenter, is known as the ship’s metacentric height.

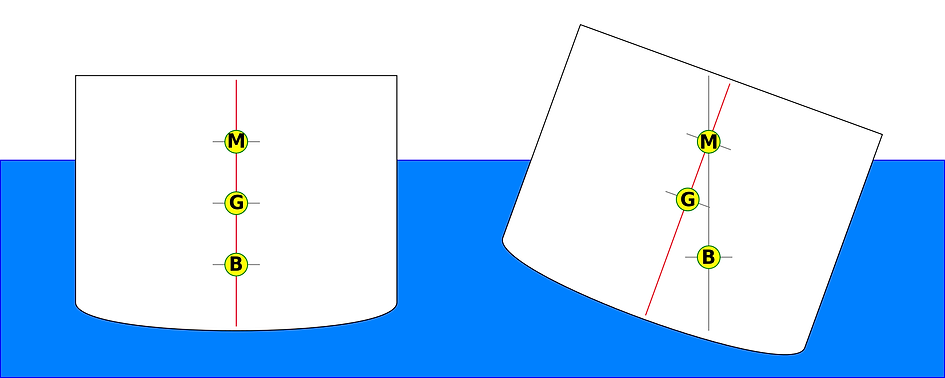
When the ship is in an upright position, the center of gravity and the center of buoyancy are aligned vertically above one another. If the ship heels to one side due to an external force, the center of gravity remains in its place relative to the ship, but it migrates to the side of the heel as a whole. The center of buoyancy migrates to the same side, into the center of the water currently displaced.

If the center of gravity and the center of buoyancy are no longer perpendicular to each other, and the center of gravity is below the initial metacenter of the ship, a so-called righting lever occurs. This righting lever creates a moment, known as the righting moment, which returns the ship to its original position. If the ship is able to return to an upright position, it is said to be in stable equilibrium.

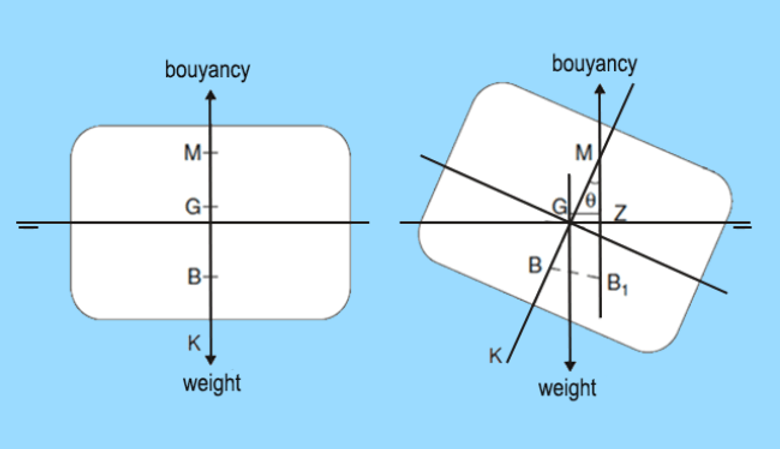
In some cases, the vertical positions of the center of gravity and the metacenter overlap, and no righting lever is created during the heel. This means that the heeling moment does not generate a righting moment to bring back the ship to its original upright position. In this case, the ship is in a neutral equilibrium.

The danger in this situation comes if there is a cargo shift, and the heeling angle of the ship is increased due to the shift of the cargo’s weight. The ship then could quickly move from a state of neutral to a state of unstable equilibrium.

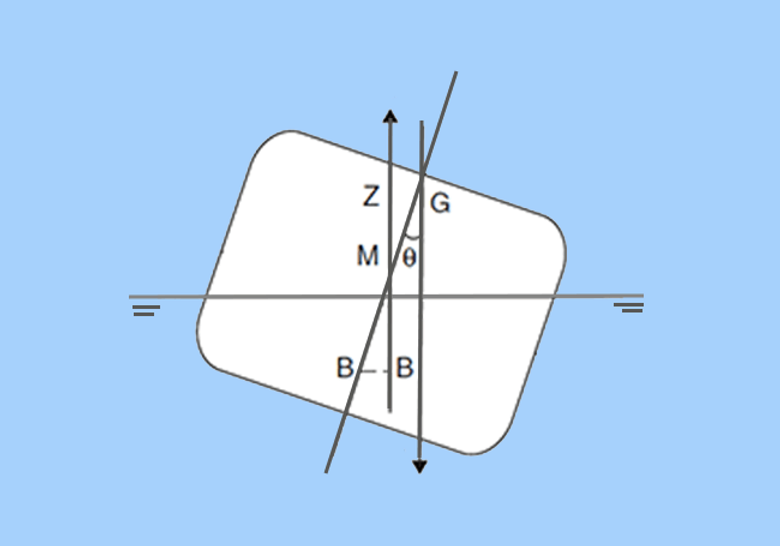
In an unstable equilibrium, the vertical position of the center of gravity is above that of the ships’ metacenter, creating a negative righting lever and thus, an even larger heel from the momentum. If the ship does not return to a stable equilibrium, and the heel increases, the ship will eventually capsize.

I hope this article helped the concepts of buoyancy and stability “sink in”. See you next time!

The Shipyard